


A non-mathematical introduction to the Fast Fourier Transform
by Richard Dobson
This document has been written for CDP at my request in order to further a deeper technical understanding of how the Phase Vocoder works. In doing so, Richard has in fact also given a general introduction to a number of important features of digital filtering. Watch for these key ideas: that the Phase Vocoder works by comparing the incoming signal with its own in-built signal; that this comparison is equivalent to a filtering operation (focusing in on a given harmonic / frequency); that the filtering process is why discussion of 'sidebands', 'aliasing', 'band-limited signals', 'Nyquist' etc. is relevant. All this may help us to anticipate a little better what may happen when we time stretch etc. and perform spectral manipulations on various types of sound. (Lastly, Richard shows how to use SPECT* and DISP* to analyze the behaviour of certain types of program, such as FILTER VARIABLE, using a 1 sample soundfile made as a control reference.) - A.E.
[* SPECT and DISP were Atari programs, no longer part of the CDP system.]
Frequency domain analysis and processing tools are arguably the most important resources available to the electronic music composer wherever the timbre of a sound is the prime concern. The most common frequency domain tool is the filter, familiar to users of both analog and digital synthesis systems. However, whereas an analog system allows filtering to be performed empirically and interactively, by moving a slider or turning a knob, with the effects immediately apparent to the ear, a general-purpose digital system such as the CDP Computer Music System is not designed with real time operation as a primary consideration. In the frequency domain especially, which is computationally demanding in a digital system, it does not allow immediate feedback (although the use of the DSP on the Atari Falcon will make this possible with certain selected operations). Filtering operations can take some time, and the composer needs to have a very precise idea of what the filter has to do, so that valuable time is not wasted by the use of either an inappropriate program or of unsuitable parameters passed to it. This document is intended to help develop the ability to assess what needs to be done.
The key to success in this task is a reliable tool for analysing the spectral character of a soundfile, which complements the sophisticated discrimination of the human ear with precise numerical analysis. The Fast Fourier Transform (FFT) is such a tool. However, the mathematical basis of its operation is all but incomprehensible to non-specialists, while its output can be misleading and confusing unless its principles are well understood. The following paragraphs present the FFT as non-mathematically as possible, yet attempt to explain it in sufficient detail for its role in the Groucho program SPECT* and in the PHASE VOCODER and its associated programs, to be understood and used effectively.
[* SPECT is no longer part of the CDP system - R.F.]
The FFT takes as its basis a principle formulated by Jean Baptiste Joseph Fourier (1768-1830). This principle is that all complex periodic waveforms (that is to say, waveforms with a clear pitch) can be modelled by a set of harmonically related sinewaves added together. Waves are said to be harmonically related when they are integer multiples of the fundamental. This is the basis of classical additive synthesis. Each sinewave corresponds to a harmonic of the fundamental frequency of the sound. The harmonic structure of a common analog waveform such as the sawtooth or square wave can be determined mathematically, and (under ideal conditions) can be precisely measured by an analysis tool such as the FFT :
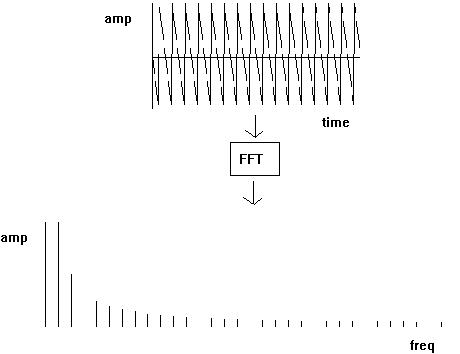
Fig 1A: downward sawtooth -> FFT -> spectrum
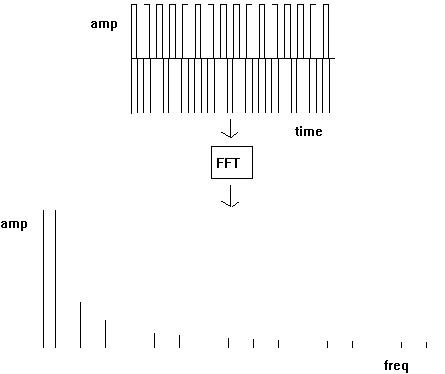
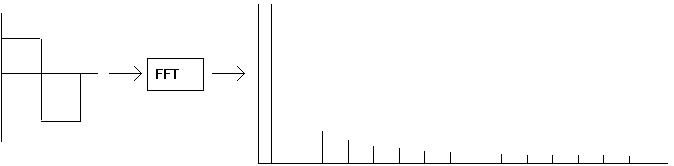
Fig 1B: square wave -> FFT -> spectrum
So, how does the FFT detect all these harmonics? It seems especially clever in the case of a square wave, which appears as far removed from the smooth shape of a sinewave as it is possible to be. It is really a case of pattern matching. The FFT is itself a periodic, harmonic-rich entity, and it detects which of its own many virtual sinewaves are also present, strongly or weakly, in the input signal by comparing its own virtual signal with the input signal. It does this form of 'pattern matching' by a process of multiplication.
When you multiply a signal by another, you are performing a 'ring modulation'. In the simplest case, the input to the ring modulator consists of two sinewaves, in which case you get two sinewaves at the output. One has a frequency equal to the numerical sum of the frequencies of the inputs, and the other is the difference between them. For example, if you multiply a sinewave at 440Hz by a sinewave at 441Hz, you get a signal consisting of a sinewave at 881Hz and a sinewave at 1Hz. Make the two inputs equal and you get an output, seemingly, of just one sinewave, at 880Hz:
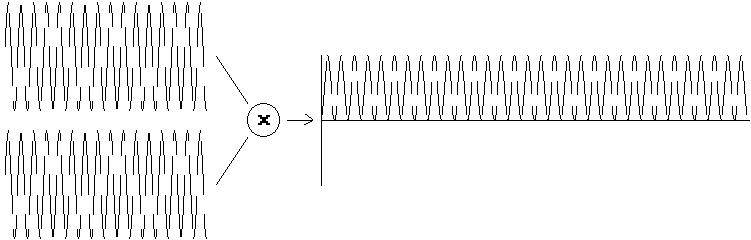
Fig 2: sine * sine -> sine
However, as the figure shows, this is not 'just' a sinewave, as it lies all above the zero line - there is a positive DC offset. This offset is directly proportional to the amplitudes of the input signals. Therefore if one of these is at a fixed 'reference' level, the output can provide a direct measure of the amplitude of the other. We can derive a value for this simply by averaging the waveform (actually a low-pass filtering process) - adding up the instantaneous amplitudes of each point of the waveform and dividing the result by the number of points. Putting it another way, the areas under the positive half of the waveform are added to the areas under the negative part. An ordinary sinewave would yield an average of zero, as the two halves cancel exactly, but the waveform in the figure above would yield a net positive value.
This process can clearly be extended in principle to arbitrary input signals by sweeping the frequency of the reference sinewave continuously though the audible range and recording the fluctuating amplitude of the output - any non-zero value signifies the presence in the input of a harmonic at that frequency and amplitude. Unfortunately, such an ideally perfect variable ring modulator is extremely difficult to design - apart from any other considerations it would probably be impossibly expensive.
Instead, we will have to make do with a digitally sampled version in the FFT. Instead of sweeping continuously through the audible range, it simply samples the input waveform at multiples of its own fundamental frequency. If this is low enough, the output will still give a good image of the spectrum of the input.
(Actually, in its mathematical guise, the Fast Fourier Transform is a streamlined version of the full Fourier Transform, which is continuous over the frequency range, and which, as a mathematical tool, enables the spectrum of a periodic geometric waveform to be determined by hand calculation. The digital version of this continuous sweep, such as might be applied to some arbitrary waveform, is the Discrete Fourier Transform. Unfortunately, this is agonisingly slow for the low fundamental frequencies we need, which is why the Fast Fourier Transform was developed. What the FFT can do in seconds, the DFT may take hours or even days to calculate!)
The frequency-sampling nature of the FFT means that it behaves just as would a bank of carefully tuned analog filters - which is what the analog spectrum analyser comprises. The more precise the measurements are to be, the narrower the pass-band of each filter must be, and the greater the number of filters required. Suppose that each filter had a bandwidth of 20Hz. It would require 1000 filters to cover the whole audio range (20 to 20,000Hz). However, this is surely overkill. Certainly, at 440Hz a bandwidth of 20Hz seems reasonable - a little less than a semitone. But at 4KHz it represents around one tenth of a semitone, unnecessary precision for most purposes.
It is hardly surprising, then, that commercial audio spectrum analysers space their filter bands not in linear (evenly spaced) frequency increments but in logarithmic (expanding) interval increments, one third of an octave being standard in professional studio equipment. (Note that the octave series relates to pitch in a logarithmic manner: more and more frequencies are contained within each (higher) octave; e.g., 220 -> 440 -> 880 -> 1760 -> 3520 etc.; thus 'one third of an octave' will span more frequencies as one goes higher.).
Unfortunately, the FFT is not economical in this way. It distributes its filters linearly across the audio range, which means that at high frequencies it is if anything too precise, but at low frequencies not precise enough to identify the pitch of a note within a semitone. This is really an unjust criticism of the FFT, since the periodic signals for which it was originally designed would not have partials that close together; it is only mentioned here because, inevitably, the FFT will be used on complex polyphonic sounds in which partials may well be as close or closer. Hence the uncertainty about what it may find between the expected harmonic partials. Used in this way, the FFT outputs what is best thought of as a statistical or general measure of the dominant pitch regions of a sound - its spectral envelope.
(A recently developed analysis and resynthesis tool, the wavelet transform, has much in common with the FFT, except that its analysis filters are spaced logarithmically. Graphical pictures of wavelet analyses correspond much more closely to the perception of the ear than does the FFT. Interested readers are directed to the article in Computer Music Journal Vol 12.4, and to the book Representations of Musical Signals, ed. Poli, Piccialli and Roads, recently published by the MIT Press.)
Although the FFT as a whole is a complex mathematical process, in terms of the filter bank model it is still rather crude. Each filter is rather simple, and does not, in fact, exclude all but a narrow band of frequencies. Each filter generates a set of sideband responses above and below the nominal centre frequency. Furthermore, the filters overlap each other. Consequently, a frequency in the input that does not sit exactly on the centre frequency of a filter will register on the outputs of several other filters on either side, a phenomenon known as 'spectral leakage'. In the figures below, the first shows the FFT analysis of a sinewave corresponding exactly to the centre frequency of one of the FFT filters; for the second figure the frequency of the signal has been moved to a point half-way between two filters. The effect on the FFT output is striking, to say the least.
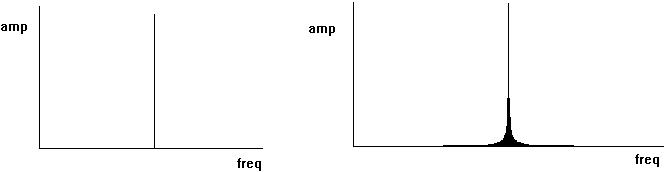
Fig 3 Fig 4
It is even worse if the vertical scale is recast in dB to show the relative power level of each filter response, rather than amplitude:

Fig 5
One could be forgiven for thinking that something was very wrong here. We might have expected two filters to register, not the mass response shown above. However, once the periodic nature of the FFT is understood, the result above will make much more sense.
(There is another consequence of spectral leakage - the maximum amplitude given by the FFT has reduced, as energy in the input signal has also leaked into adjacent filters. It is not very much - around 3dB on average, but it shows that, sometimes, the amplitude values of spectral peaks in the FFT may have to be taken with a small pinch of salt - some signals may be significantly stronger than the FFT suggests. Note also, when using SPECT, that if you want the FFT output to reflect the absolute (actual) signal level with respect to frequency, you need to use the -u flag, otherwise for display purposes the output will be normalised (i.e., 'scaled' to the maximum amplitude range) by setting the highest spectral peak to maximum amplitude and adjusting the other values accordingly.)
At this point we need to look a little more closely at the practical implementation of the FFT. Intuitively we can see that while we can quite reasonably speak of the instantaneous amplitude of a signal (simply a single sample value), we cannot so easily speak of instantaneous frequency. Experiments in psycho-acoustics have established that the ear cannot recognise the pitch of a sound until it is at least some 20msecs long (0.023 sec). Imagine an amplifier with a faulty connection - somewhere the signal is continuous but we only hear intermittent blips. Unless these blips are 20msecs or more, we cannot hear a pitch, only a click. If we wanted to identify what instrument was playing, we would need much longer blips - even half a second might not be enough.
These blips are, in effect, short windows onto the sound. The input to the FFT is such a window - a short block of samples. At a sample rate of 22050 per second, a block of 256 samples represents just over 23msecs, and is arguably the shortest useful window length for the FFT (note also its fundamental frequency: 22050/256 = 86.1Hz, which is rather high – about F immediately below the bass clef). In the figures below, a short signal is shown with an FFT window superimposed on it; the second figure shows the window portion separately, as the FFT sees it.
Note that this 'window' is a rectangular shape, cutting through the wave wherever the edge of the window falls, irrespective of whether the value at the edge is non-zero. This means that abrupt changes of amplitude may and probably will take place at these edges, as one window follows another -- and these abrupt changes can cause clicks in the sound.
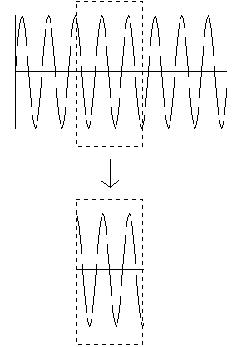
Fig 6 (upper) and Fig 7 (lower)
We can see that the signal is a sinewave, and might intuitively expect the FFT analysis to show one spectral line. However, the FFT assumes that its window is equivalent to exactly one cycle of a periodic waveform, so it thinks the waveform really looks like Fig 8 (the waveform's periods are formed by a series of its analysis windows). Note the irregularities in what should be a smooth sinewave and how the pattern repeats -- these show the edges of the analysis windows:
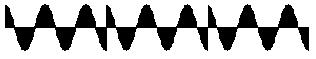
Fig 8
Clearly this would not sound anything like a sinewave! The output of the FFT now seems much more understandable, if annoying.
Looking at the contents of the window, we can see clearly that the problem is caused by the discontinuity between the ends of the windowed signal. The FFT is, so to speak, out of tune with the input signal. In fact, the chances of the FFT window ever being exactly in tune with the input signal are fairly remote - we can safely assume that such discontinuities will be the rule, not the exception.
It seems reasonable to suppose that if we could somehow squash the ends of the window to reduce the discontinuity, the FFT might not be upset so much. This is indeed what is done. The window function most commonly used is the Hamming Window, which is illustrated below, together with the FFT analysis of the signal used previously, multiplied beforehand by the Hamming Window. (The illustration of the Hamming window is an approximation.)
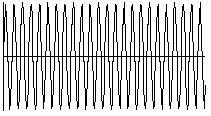
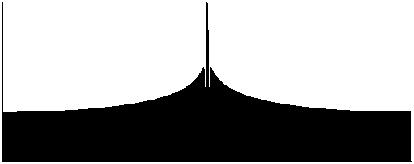
Fig 9: plain wave Fig 10: Hamming windowed wave Fig 11: FFT
Although it is not perfect, it is clearly a great improvement on before, which used a rectangular window. Note that the program SPECT* offers the option to use a rectangular window instead of the Hamming Window, and the companion display program DISP* can plot the FFT either as a spectral envelope or as discrete spectral lines, so this combination is ideal for experimentation. The Phase Vocoder does not include a rectangular window option.
[* SPECT and DISP are no longer part of the CDP system - R.F.]One side effect of the use of the Hamming or similar window is that partials which are exact harmonics of the FFT fundamental frequency will now no longer show up as single spectral lines (the input has, in effect, been amplitude modulated: the amplitude is made to rise from and fall to zero at the edges of the window); it is, however, a price well worth paying, especially given the rarity of exact harmonics in 'real' signals.
From the above it would seem that a long window of, say, 1024 samples, has to be better than one of 256 samples, as the frequency resolution is so much better. This is indeed true, but it is also important to remember that at the low sample rate (22050), 1024 samples represents some 46msecs (ie just under a 20th of a second: 1024 samples \ 22050 sr = 0.046 sec), during which quite a lot can happen, especially if you are analysing something such as the attack of a trumpet, or of a percussive sound.
A long window has better frequency resolution but worse time resolution. In the Phase Vocoder this dilemma is resolved to a great extent by overlapping the windows. For example, using a window of 1024 samples, successive FFTs will be applied to windowed portions starting at sample 1, 64, 128, 192, 256, and so on, moving through the sound in steps of 64 samples, whilst creating frames of 1024 samples. In this case the analysis sampling rate has octupled, from 21.53Hz to 172.26Hz, or from 46msec steps down to around 5msecs. Only for zero overlap is the analysis sampling rate equal to the fundamental frequency of analysis. However, this is not satisfactory in the case of the Phase Vocoder, because of the use of the Hamming window, which requires that there be an overlap of at least two for the original waveform to be reconstructed exactly.
From the above it is clear that frequency resolution is one of the most important parameters of the FFT. With the Phase Vocoder, this can indeed be specified directly, up to a point, by setting the F flag to some value. The Phase Vocoder warns that you cannot set both F and N (the length of the analysis window in samples), showing that these flags are intimately related alternative ways of controlling one parameter.
Specifying window length (N) In both SPECT and the Phase Vocoder it is recommended that the window length for the analysis be a power of two - for example, 256, 512 or 1024 samples. This is because the FFT algorithm is particularly efficient with such values - when you are doing probably hundreds or thousands of FFT's in the Phase Vocoder you would need a very good reason indeed not to use the fastest type of FFT algorithm possible.
However, the FFT can work with other window lengths, and will still be fairly efficient so long as the length is very 'composite' - has a large number of factors. Thus a length of, say, 384 (= 2*4*6*8) would also work very well. In the worst case, a number with few or no factors would reduce the FFT to the DFT, which as explained above is very, very, slow. It would be sensible to go on a world cruise, or a three-year Buddhist retreat, if you apply the DFT to a long soundfile.
Specifying Frequency (F) The reason that the F option is available at all is that you may well want to 'tune' the FFT as closely as possible to a known fundamental frequency in your soundfile. Instead of defining the window length, you can define the desired fundamental frequency, and the nearest available window length will be selected for you. The one constraint is that the window length be even.
Thus, if you ask the Phase Vocoder to tune itself to 50Hz, it could do so exactly if the window length was able to be 441 samples long (22050 sr \ 50Hz = 441 samples); this is in fact rounded up internally to 442 samples - not, as it happens, an ideal length for a window, as explained above. You will almost certainly find it more sensible to calculate what the ideal window length should be, and then give the FFT the nearest efficient length.
For example, if you want to tune to 440Hz (at the low sample rate) the nearest integer window length will be 50 (rounded down from 50.1 -- 22050 sr \ 440Hz = 50.1 samples). A much better window length would be 54, and, of course, a length of 64 would be the most efficient of all. An alternative course of action, if you really want the greatest accuracy possible, is to tune the soundfile to the FFT (ie to transpose it using FTRANS). Anyone who seriously wants to do this can probably work out the transposition ratios for themselves!
There is one feature of the FFT that has proved a potential source of confusion. The number of 'channels' output by the FFT is usually stated as being half the number of samples in the window. For example, a window of 1024 samples results in an FFT output of 512 channels. There is in fact a very simple explanation for this, which relates directly to the question of the highest frequency which can be accommodated by a given sample rate. It requires a minimum of two samples to represent a single cycle of a sinewave - one positive and one negative. Thus, the maximum frequency which can be represented in a digital soundfile is exactly half the sample rate (the Nyquist limit). The FFT behaves in the same way - it takes N samples and outputs N/2 channels.
Behind this explanation lies a very important mathematical assumption - that the input signal is 'real'. The terms 'real' and 'imaginary' crop up frequently in digital signal processing, and belong to the mysterious world of 'complex' numbers (see, for example, the documentation for SPECT).
In a much simplified way of understanding the relationship between 'real' and 'imaginary', a sinewave is considered as an 'imaginary' signal and a cosine wave as 'real'. A complex number comprises both a real and an imaginary part. If you imagine a graph with the sine function on the Y-axis (up-down) and the cosine function on the X-axis (right-left), then a complex number equates to the co-ordinates of a point on that graph. Alternatively, this point can be specified in terms of an amplitude (radial distance from the origin) and an angle, measured from the X axis. This 'polar' representation is widely used in signal processing, and is central to the operation of the FFT.
All that is really going on here is a need to recognise the phase of the input signal. A sinewave is simply a cosine wave shifted to the right a quarter of a cycle. Without the use of both sine and cosine waves in the FFT we would not be able to tell what are the relative phases of all the components of the input. Some may be pure sinewave, others pure cosine wave, but the majority (perhaps all) will be somewhere in-between; that is, the frequency components start at different places in the cycle.
For simple analysis purposes this does not matter very much, but it does matter as soon as we want to recreate the waveform from the channel data, as is done in the Phase Vocoder. Here we are not only recreating the data in one window, we are recreating several overlapping windows. Clearly the phase must be continuous from one window to the next, otherwise there will be gross discontinuities in the output.
Phase information is generally not of great relevance to the musician, and you may never need to trouble yourself with it, but it exists as an inevitable consequence of the FFT process. To put this another way, there is no information lost by the FFT, so that applying the 'inverse FFT' to the unmodified spectral data will recreate the original waveform exactly. Needless to say, this is a musically pointless exercise - the great strength of the Phase Vocoder and its associated programs is that it allows the composer to manipulate the spectral content of a complex input signal in arbitrary ways. The fact that it may be difficult to interpret a single FFT output of a spectrally complex input does not mean that the information has somehow got lost or damaged in some way - it simply means that it is difficult to interpret!
In the Phase Vocoder an additional channel centred on 0Hz is generated. This serves to register signals below the fundamental frequency of the FFT more precisely than the 'raw' FFT can manage. In the latter, any wavecycle too long for the FFT window will register as a signal at the fundamental frequency (ie not at DC), together with a considerable number of sideband responses. The extra channel seems to help in the alignment of near-DC phase between FFTs and thus improve low frequency resolution and continuity. If you study 'pvoc.s', the file created by the Phase Vocoder using the -V flag, you will see that this first channel has a low boundary of negative frequency, for example -43Hz to +43Hz. A negative frequency corresponds to an inversion of phase. Thus the first channel tracks the phase of any sub-fundamental signal across the overlapping FFTs.
As mentioned above, the FFT is directly invertible - the original waveform can be reconstructed exactly. This is still true to a great extent even where there is such a sub-fundamental component in the input. The problems really show up when the re-synthesis is combined with something like time-stretching (one of the primary applications of the Phase Vocoder) - the result will be lumpy, probably full of glitches, and the pitch content of the output will not bear much relation to the input.
Any mention of the Nyquist limit reminds us of the importance of ensuring that all signals which are to be sampled or processed digitally need to be 'band-limited': that is, there must be no signal components higher than half the sample rate. Being markedly permissive, the CDP System takes few, if any, steps to prevent this happening. For example, it is very easy to drive ADSYN into aliasing by editing the text file that it creates; this is done simply by changing some of the frequency values to lie above the Nyquist limit of sr/2. If you want to demonstrate aliasing to somebody, this is probably the easiest way to do it. Similarly, any upwards transposition can result in aliased components. For this reason, a precautionary low-pass filtering operation is always advisable before doing such a transposition: to remove the higher components which could alias. If there is a signal with high energy components and aliasing is experienced when it is transposed, the rule of thumb is to low-pass filter the original by Nyquist / transposition interval and transpose again. Also, only generate sounds with frequencies up to sr/2.
Aliasing can however be induced simply by creating any non bandlimited waveform, of which the square wave is the most common example. A 'true' square wave has an infinite number of partials, though the high ones are then infinitely small. Unfortunately, enough of them are large enough to cause a problem even at low frequencies. The first figure below shows one cycle of a square wave, together with its FFT (using a 1024-sample rectangular window). The amplitude of the high partials just about falls to inaudibility at the Nyquist limit. At the low sample rate, this signal would have a pitch of 21.5Hz.
[Fig 12: square wave -> FFT]
Compare this with the next figure - the pitch has risen three octaves to 64.5Hz - still quite low, but the aliasing already shows up very clearly:
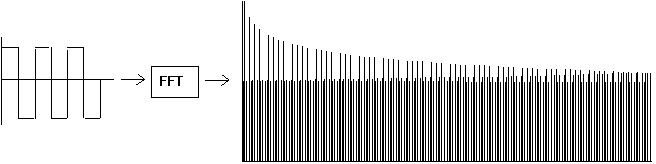
Fig 13: 3-cycle square wave -> FFT
This shows the periodic nature of the sampled spectrum very clearly - any alias components 'wrap around' both the Nyquist limit and DC and appear as lower spectral components.
In fact, the aliasing is present even in the previous figure, but the alias components fall in already occupied channels - there is constructive interference. The result is that the harmonics appear stronger than they really are.
In both figures, the square wave fits the FFT window exactly - there is no spectral leakage. If, however, the signal did not fit exactly, as is most likely, most if not all of the alias components would be swamped by the spectral leakage:

Fig 14: 17.5 cycle square wave -> FFT
At the beginning ot this text, mention was made of the need to be very clear about the effect of a filter on a soundfile. It would seem that the only way to do this is to run a filter with a set of parameters, listen to the result (and perhaps check it with the FFT), and if it is not right, alter the parameters and repeat the process. This is time-consuming, especially if the filter operation takes a long time. Also, as we have seen, the FFT itself can be difficult to interpret - typically, the FFT outputs a great deal of 'noise', implying the use of a stronger filter than is really necessary. Another problem is that many of the CDP filter programs do not reliably apply exactly the levels of cut or boost that you have specified. Testing them directly on a complex soundfile would be impractical and also confusing, as you would need to correlate the output with the input to ascertain exactly what effect the filter is having. Testing a filter with a noise source is better, but still not ideal.
This section suggests an alternative to the above. Fortunately the FFT can itself be used to test a filter directly, and very quickly. All that is needed is a reference soundfile for testing. This would be a short soundfile containing an impulse - a single sample of maximum amplitude, followed by a suitable number of zero samples. One possible way to make this reference soundfile is to extract a single sample by setting marks in VIEWSF's a mode (set the marks with the Function keys), cut out this sample with CUT and marks.dat (which will be automatically created when you exit VIEWSF). Then mix your one-sample soundfile with a short soundfile of SILENCE (made with SIGNAL or WAVE). This soundfile can now be used for all your tests.
STEP 1 - Run the filter program to be tested with the impulse soundfile, using the parameters you thought would work with the big soundfile you intend to filter; the resulting soundfile reveals that filter's impulse response: The example below used FSTATVAR [now FILTER VARIABLE] and the following parameters: low-pass, a centre frequency of 440, Q of 1 (1 in this case because a very compact display was needed; normally Q will be somewhere between 1 and 100), and a gain of 1.
STEP 2 - The resulting soundfile is then displayed by VIEWSF.
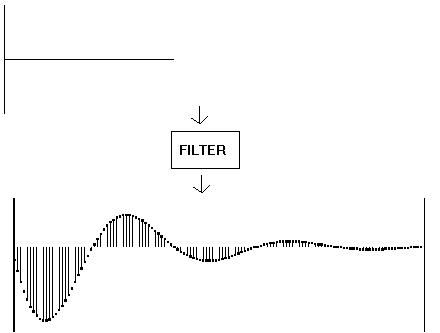
Fig 15: impulse soundfile -> filter (FSTATVAR) -> impulse response (seen with VIEWSF)
STEP 3 - We can now apply the FFT to this, using SPECT with the impulse response option (the -f flag), and the output gives the frequency response of the filter:
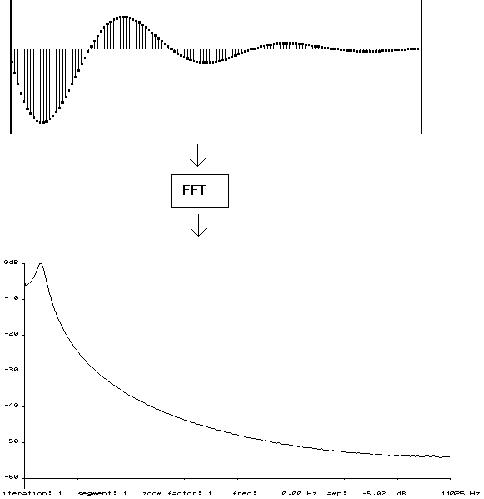
Fig 16: impulse response (seen with VIEWSF) -> FFT (SPECT) -> freq. response (seen with DISP)
STEP 4 - Display with DISP. Note that, at present, DISP cannot recognise the output of SPECT using the -f flag. You can use the 'crude' screen plot of SPECT itself, or run SPECT using the -d and -r flags (the latter setting a rectangular window); the output from this can then be displayed by DISP. Check the length of the impulse response using VIEWSF, and make sure that you set an FFT window large enough to accommodate it. A 1024-sample window should cover all but exceptional cases.
The DISP display graphically illustrates the amplitude roll-off across the range of frequencies. This should provide a reasonable idea of what will happen if you use the same filter with the same parameters to your original soundfile. Over a period of time, this procedure should build up a more accurate understanding of the behaviour of various programs.
One final point. Remember that SPECT normalises the output unless the -u flag is used (see p.5 above). To see the actual peak response of the filter, therefore, use the -u flag so that the peak isn't normalised to maximum on the display -- if the peak is at -10dB, we need to know that!
In principle, this method of testing the results can be applied to any program that generates multiple output samples for a single input (ie, based on some form of delay process). This includes programs such as ALLPASS, DELAY (short delays create comb filters), and even reverb programs such as the one in CSOUND.
Richard Dobson
Frome, Somerset
June 1993
© 1993 Richard Dobson & CDP